三角形的欧拉线方程怎么求_三角形中的欧拉公式

2024-10-12 17:52:26

1.求初中数学的课外公式，比如欧拉公式

2.欧拉公式如何将三角函数与指数函数联系起来的？

3.什么是欧拉公式

4.四个欧拉公式是什么?

三角形的欧拉线方程怎么求_三角形中的欧拉公式

已知三角形ABC中，外接圆圆心O，半径R。内接圆圆心I，半径r。设d为O到I的距离。求证：d?=R(R-2r).

设角OAB=q，

r=(R+d)sinq, r+d=Rcos2q

再由cos2q=1-2(sinq)?，得到(d+R+r)[d?-R(R-2r)]=0

因为OI<OA,d又不等于-R-r，所以d?-R(R-2r)=0

所以d?=R(R-2r)

求初中数学的课外公式，比如欧拉公式

R+ V- E= 2就是欧拉公式。

在任何一个规则球面地图上，用 R记区域个数，V记顶点个数，E记边界个数，则 R+ V- E= 2，这就是欧拉定理?，它于 1640年由 Descartes首先给出证明。

后来 Euler(欧拉 )于 1752年又独立地给出证明，我们称其为欧拉定理，在国外也有人称其为 Descartes定理。

扩展资料：

数学归纳法证明：

1、当 R= 2时，由说明 1,这两个区域可想象为以赤道为边界的两个半球面，赤道上有两个“顶点” 将赤道分成两条“边界”，即 R= 2，V= 2，E= 2；于是 R+ V- E= 2,欧拉定理成立.。

2、设 R= m(m≥ 2)时欧拉定理成立，下面证明 R= m+ 1时欧拉定理也成立。

由说明 2，我们在 R= m+ 1的地图上任选一个区域 X ,则 X 必有与它如此相邻的区域 Y ，使得在去掉 X 和 Y 之间的唯一一条边界后，地图上只有 m 个区域了。

在去掉 X 和 Y 之间的边界后，若原该边界两端的顶点现在都还是 3条或 3条以上边界的顶点。

则该顶点保留，同时其他的边界数不变;若原该边界一端或两端的顶点现在成为 2条边界的顶点，则去掉该顶点 ,该顶点两边的两条边界便成为一条边界。于是 ,在去掉 X 和 Y之间的唯一一条边界时只有三种情况：

1、减少一个区域和一条边界。

2、减少一个区域、一个顶点和两条边界。

3、减少一个区域、两个顶点和三条边界。

百度百科——欧拉公式

欧拉公式如何将三角函数与指数函数联系起来的？

1、欧拉（Euler）线：

同一三角形的垂心、重心、外心三点共线，这条直线称为三角形的欧拉线；且外心与重心的距离等于垂心与重心距离的一半

2、九点圆：

任意三角形三边的中点，三高的垂足及三顶点与垂心间线段的中点，共九个点共圆，这个圆称为三角形的九点圆；其圆心为三角形外心与垂心所连线段的中点，其半径等于三角形外接圆半径的一半。

3、费尔马点：

已知P为锐角△ABC内一点，当∠APB＝∠BPC＝∠CPA＝120°时，PA＋PB＋PC的值最小，这个点P称为△ABC的费尔马点。

4、海伦（Heron）公式：

在△ABC中，边BC、CA、AB的长分别为a、b、c，若p＝（a＋b＋c），则△ABC的面积S

5、塞瓦（Ceva）定理：

在△ABC中，过△ABC的顶点作相交于一点P的直线，分别交边BC、CA、AB与点D、E、F，则；其逆亦真

6、密格尔（Miquel）点：

若AE、AF、ED、FB四条直线相交于A、B、C、D、E、F六点，构成四个三角形，它们是△ABF、△AED、△BCE、△DCF，则这四个三角形的外接圆共点，这个点称为密格尔点。

7、葛尔刚（Gergonne）点:

△ABC的内切圆分别切边AB、BC、CA于点D、E、F，则AE、BF、CD三线共点，这个点称为葛尔刚点。

8、西摩松（Simson）线：

已知P为△ABC外接圆周上任意一点，PD⊥BC，PE⊥ACPF⊥AB，D、E、F为垂足，则D、E、F三点共线，这条直线叫做西摩松线。

9、黄金分割：

把一条线段(AB)分成两条线段,使其中较大的线段(AC)是原线段(AB)与较小线段(BC)的比例中项,这样的分割称为黄金分割

10、勾股定理：

即直角三角形两直角边的平方和等于斜边的平方。这是平面几何中一个最基本、最重要的定理，国外称为毕达哥拉斯定理。

11、笛沙格（Desargues）定理：

已知在△ ABC与△A'B'C'中，AA'、BB'、CC'三线相交于点O，BC与B'C'、CA与C'A'、AB与A'B'分别相交于点X、Y、Z，则X、Y、Z三点共线；其逆亦真。

12、摩莱（Morley）三角形：在已知△ABC三内角的三等分线中，分别与BC、CA、AB相邻的每两线相交于点D、E、F，则三角形DDE是正三角形，这个正三角形称为摩莱三角形。

13、帕斯卡（Paskal）定理：已知圆内接六边形ABCDEF的边AB、DE延长线交于点G，边BC、EF延长线交于点H，边CD、FA延长线交于点K，则H、G、K三点共线

14、托勒密（Ptolemy）定理：

在圆内接四边形中，AB?CD＋AD?BC＝AC?BD

15、阿波罗尼斯（Apollonius）圆一动点P与两定点A、B的距离之比等于定比m：

n，则点P的轨迹，是以定比m：

n内分和外分定线段的两个分点的连线为直径的圆，这个圆称为阿波罗尼斯圆，简称“阿氏圆”

16、梅内劳斯定理

17、布拉美古塔（Brahmagupta）定理：

在圆内接四边形ABCD中，AC⊥BD，自对角线的交点P向一边作垂线，其延长线必平分对边

什么是欧拉公式

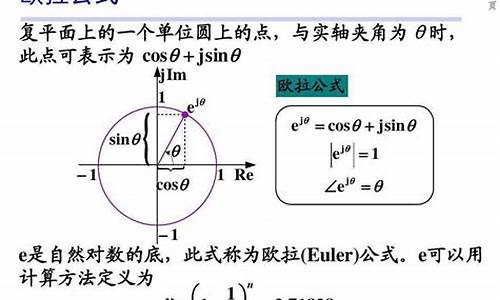
欧拉公式是数学中的一个重要公式，它将三角函数与指数函数联系起来。欧拉公式的表达式为：e^(ix)=cosx+isinx，其中i是虚数单位，x是实数。

首先，我们需要了解三角函数和指数函数的定义。三角函数是一类特殊的函数，它们在直角三角形中定义，包括正弦函数sin、余弦函数cos和正切函数tan。指数函数是一类以常数e为底的幂函数，表示为a^x，其中a是常数，x是实数。

欧拉公式的左边是复数形式的指数函数，右边是三角函数的形式。我们可以将欧拉公式进行一些变换来理解它的意义。首先，我们可以将等式两边同时乘以i，得到：-i*e^(ix)=-isinx+icosx。然后，我们可以将等式两边同时除以-i，得到：e^(ix)=sinx-icosx。这个等式表明，复数形式的指数函数可以表示为一个实部和一个虚部的乘积，其中实部是正弦函数，虚部是余弦函数的负值。

接下来，我们可以将欧拉公式进行一些代数运算来进一步理解它的意义。首先，我们可以将等式两边同时乘以e^(-ix)，得到：1=e^(ix)(e^(-ix))=(cosx+isinx)(cosx-isinx)=cos^2x-sin^2x=1-2sin^2x。这个等式表明，指数函数的模长等于1减去2倍的正弦函数的平方。

此外，我们还可以发现欧拉公式的一些特殊性质。例如，当x=π/2时，欧拉公式变为：e^(iπ/2)=cosπ/2+isinπ/2=i。这个等式表明，当角度为π/2时，复数形式的指数函数表示为虚数单位i。

综上所述，欧拉公式通过将三角函数与指数函数联系起来，为我们提供了一种统一的视角来理解和研究这两个重要的数学概念。它不仅揭示了三角函数和指数函数之间的深刻联系，还为我们解决一些复杂的数学问题提供了有力的工具和方法。

四个欧拉公式是什么?

欧拉公式是欧哈德·欧拉在十八世纪创造的，是数学界最着名、最美丽的公式之一。之所以如此，是因为它涉及到各种显然非常不同的元素，比如无理数e、虚数和三角函数。复变函数中，e^(ix)=(cos x+isin x)称为欧拉公式，e是自然对数的底，i是虚数单位。

欧拉公式有4条，分别是：

1、分式

a＾r/（a-b）（a-c）+b＾r/（b-c）（b-a）+c＾r/（c-a）（c-b）

当r=0，1时式子的值为0；当r=2时值为1；当r=3时值为a+b+c。

2、复数

由e＾iθ=cosθ+isinθ，得到：sinθ=（e＾iθ-e＾-iθ）/2i；cosθ=（e＾iθ+e＾-iθ）/2此函数将两种截然不同的函数---指数函数与三角函数联系起来，被誉为数学中的“天桥”。

当θ=π时，成为e＾iπ+1=0 它把数学中最重要的e、i、π、1、0联系起来了。

3、三角形